Welcome back! In Probability 101, we explored the counter-intuitive Monty Hall problem. Today, we’re diving into another classic of probability theory: the Birthday Problem.

While most people are familiar with the “classic” version—how many people do you need in a room for two of them to share a birthday?—it turns out there are several variations of this problem, each with its own surprising result.

In this post, we will look at four different variations, simulating them with Python and then deriving their analytical solutions.

1. Matching a Predefined Birthday

The first variation is simple: Given a specific date (say, January 1st), how many students do you need in a classroom so that the probability of at least one student having that birthday is $\ge 0.5$?

Python Simulation

We can model this by generating $n$ random birthdays (from 0 to 364) and checking if our predefined day is among them.

import numpy as np

def problem_1(n_students):
    # Predefine a specific birthday (e.g., day 0)
    predef_bday = np.random.randint(0, 365)
    
    # Generate birthdays for every student
    gen_bdays = np.random.randint(0, 365, (n_students))
    
    # Check if predefined bday is among students
    return predef_bday in gen_bdays

Running this simulation for various classroom sizes gives us the following result:

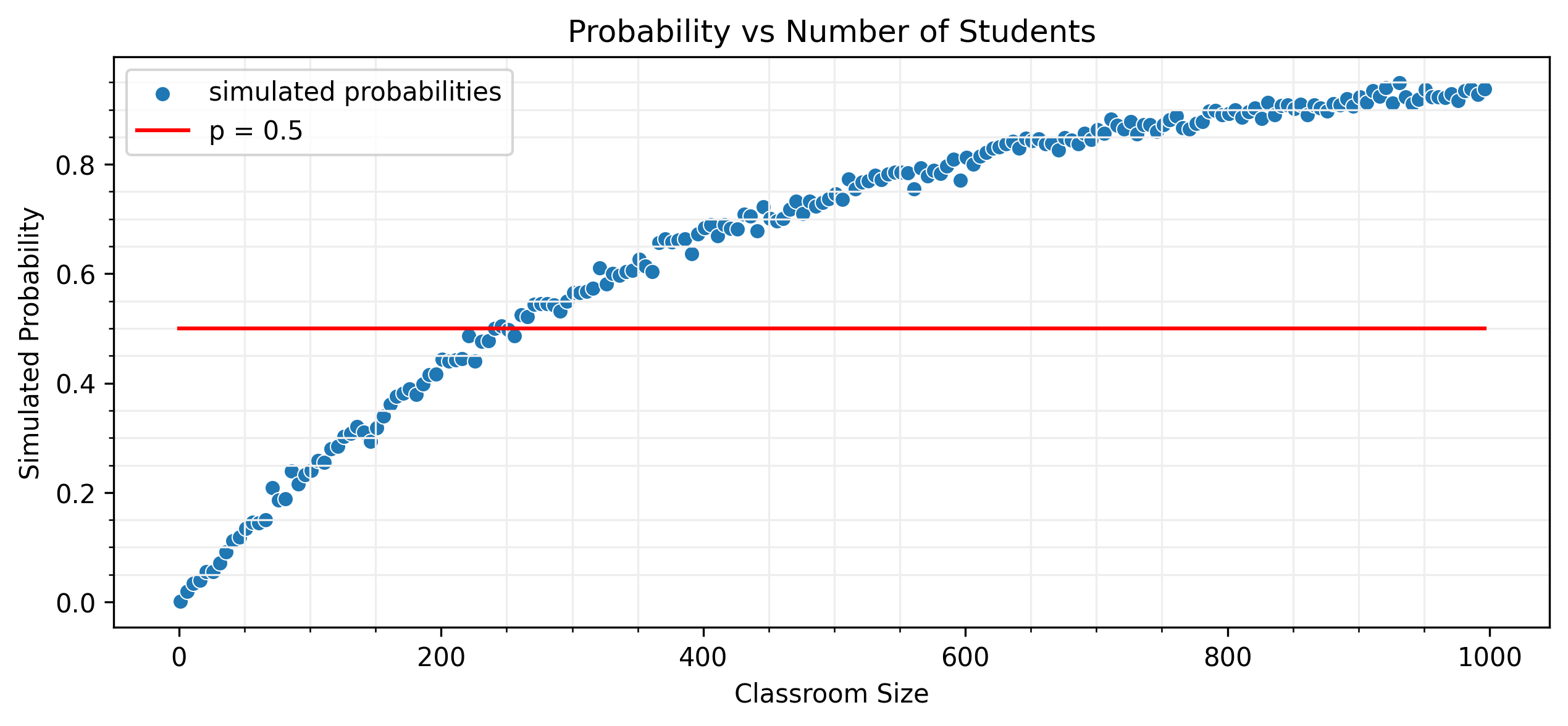
Simulation Results for Problem 1

Analytical Solution

Let $n$ be the number of students. The probability that a student doesn’t have the predefined birthday is $\frac{364}{365}$. Since student birthdays are independent, the probability that none of the $n$ students have that birthday is:

$$Q = \left(\frac{364}{365}\right)^n$$

The probability of at least one match is $P = 1 - Q$:

$$f(n) = 1 - \left(1 - \frac{1}{365}\right)^n$$

To find $n$ for $f(n) \ge 0.5$:

$$1 - \left(\frac{364}{365}\right)^n \ge 0.5$$

$$\left(\frac{364}{365}\right)^n \le 0.5$$

$$n \log\left(\frac{364}{365}\right) \le \log(0.5)$$

$$n \ge \frac{\log(0.5)}{\log(364/365)} \approx 253$$

So, you need 253 students for a 50% chance of a match.

2. Matching a Random Student’s Birthday

In this variation, we pick one student from the classroom at random. What is the probability that at least one other student shares that same birthday?

Python Simulation

def problem_2(n_students):
    # Generate birthdays for every student
    gen_bdays = np.random.randint(0, 365, (n_students))
    
    # Pick one student at random
    rnd_index = np.random.randint(0, len(gen_bdays))
    rnd_bday = gen_bdays[rnd_index]
    
    # Remove that student from the pool
    remaining_bdays = np.delete(gen_bdays, rnd_index, axis=0)
    
    # Check if another student shares the same bday
    return rnd_bday in remaining_bdays

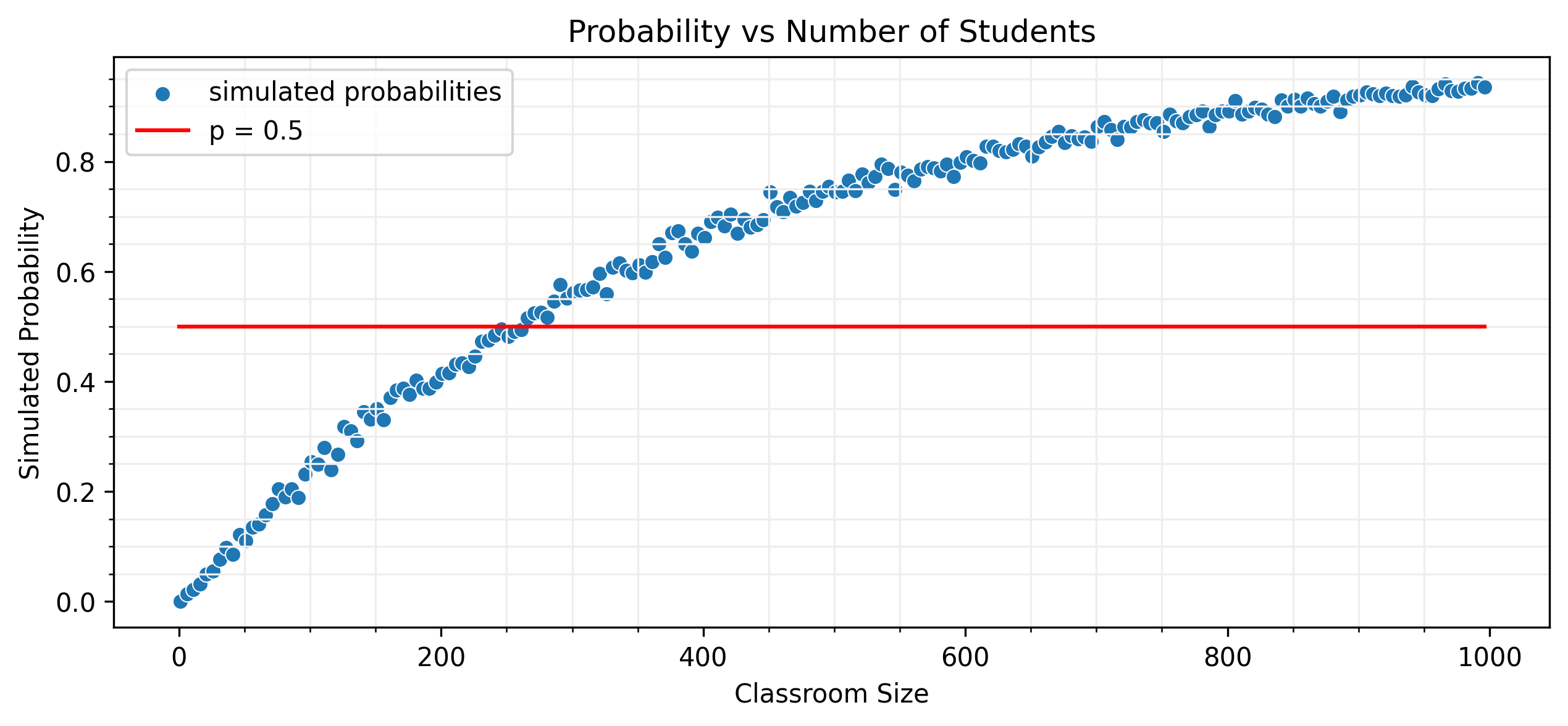
Simulation Results for Problem 2

Analytical Solution

This is subtly different from Problem 1. Instead of a fixed date, we have a classroom-dependent date. However, since the first student’s birthday is just some day $D$, the problem reduces to finding a match for day $D$ among the remaining $n-1$ students.

$$f(n) = 1 - \left(1 - \frac{1}{365}\right)^{n-1}$$

Following the same logic as before, $n-1 \ge 253$, so $n \ge 254$. You need 254 students here.

3. The Classic Birthday Problem

This is the version most people know: What is the probability that any two students in a classroom share a birthday?

Python Simulation

def problem_3(n_students):
    # Generate birthdays for every student
    gen_bdays = np.random.randint(0, 365, (n_students))
    
    # If the number of unique birthdays is less than n, there is a match
    return len(np.unique(gen_bdays)) != len(gen_bdays)

The result is much more dramatic:

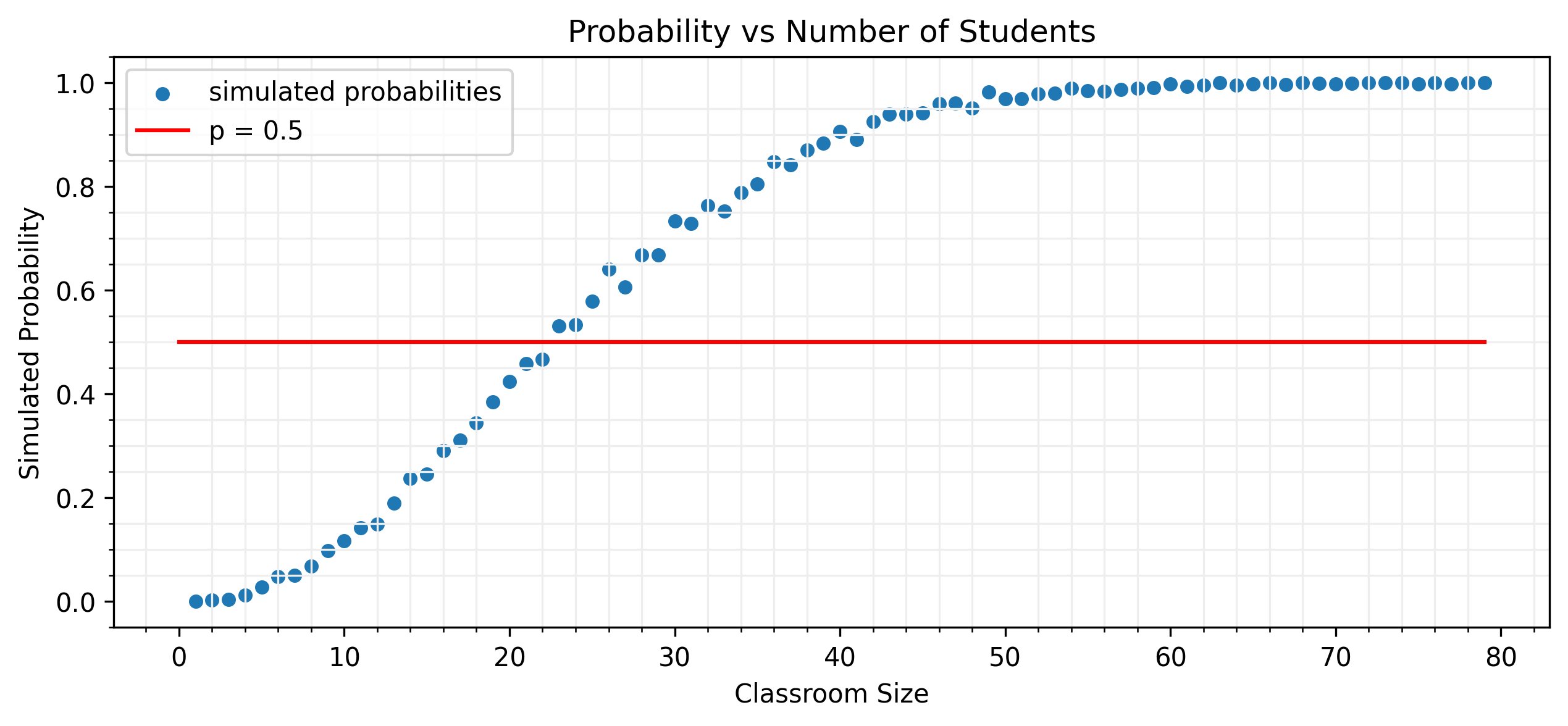
Simulation Results for Problem 3

Analytical Solution

The probability that $n$ students all have different birthdays is:

$$Q = 1 \cdot \frac{364}{365} \cdot \frac{363}{365} \cdot \ldots \cdot \frac{365 - (n-1)}{365} = \frac{365!}{365^n (365-n)!}$$

Using the approximation $1 - x \approx e^{-x}$, we get:

$$Q \approx e^{-1/365} \cdot e^{-2/365} \cdots e^{-(n-1)/365} = e^{-\frac{n(n-1)}{730}}$$

Setting $Q \le 0.5$ leads to $n \approx 23$. Only 23 students are needed! This is a classic example of how “collisions” become likely much faster than we expect.

4. Matching Between Two Classrooms

Finally, consider two separate classrooms, each with $n$ students. What is the probability that at least one student from the first classroom shares a birthday with at least one student from the second classroom?

Python Simulation

def problem_4(n_students):
    # Generate birthdays for both classrooms
    gen_bdays_1 = np.random.randint(0, 365, (n_students))
    gen_bdays_2 = np.random.randint(0, 365, (n_students))
    
    # Check for any match between both classrooms
    return np.isin(gen_bdays_1, gen_bdays_2).any()

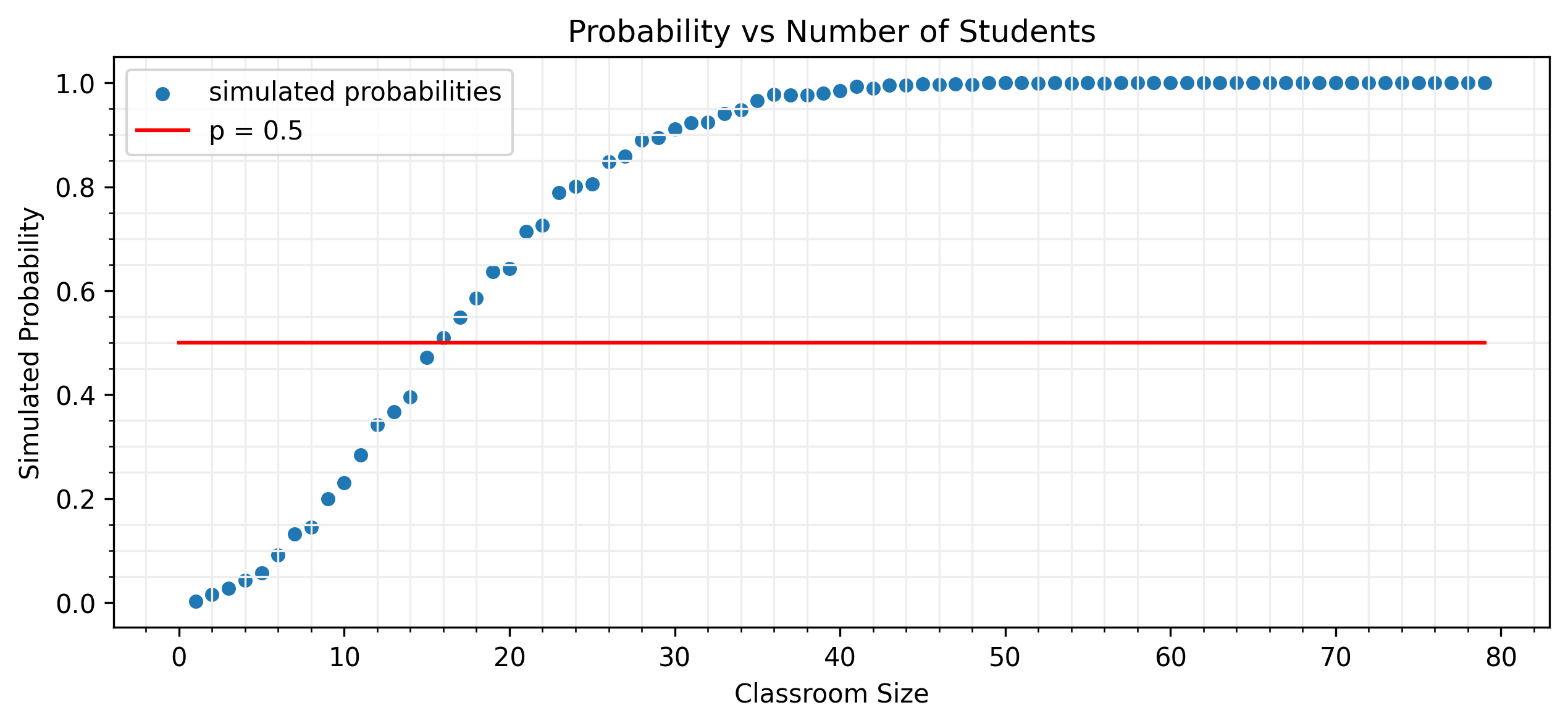
Simulation Results for Problem 4

Analytical Solution

Similar to Problem 1, but now we have $n$ target dates. The probability that no student in the second classroom matches any of the $n$ students in the first classroom is:

$$Q = \left( (1 - 1/365)^n \right)^n = (1 - 1/365)^{n^2}$$

Using the same approximation:

$$Q \approx e^{-n^2/365}$$

Setting $Q \le 0.5$:

$$n^2 \ge 365 \ln(2) \approx 253$$

$$n \ge \sqrt{253} \approx 15.9$$

So, you only need 16 students in each classroom for a 50% chance of a match between them!

Conclusion

The Birthday Problem illustrates a fundamental concept in probability: when you look for any match among a group, the number of possible pairings grows quadratically with the group size. This is why the “Classic” and “Two Classroom” variations require so few people compared to matching a specific date.

Happy simulating!